PRML读书会第四章 Linear Models for Classification
主讲人 planktonli
planktonli(1027753147) 19:52:28
现在我们就开始讲第四章,第四章的内容是关于 线性分类模型,主要内容有四点:
1) Fisher准则的分类,以及它和最小二乘分类的关系 (Fisher分类是最小二乘分类的特例)
2) 概率生成模型的分类模型
3) 概率判别模型的分类模型
4) 全贝叶斯概率的Laplace近似
需要注意的是,有三种形式的贝叶斯:
1) 全贝叶斯
2) 经验贝叶斯
3) MAP贝叶斯
我们大家熟知的是 MAP贝叶斯
MAP(poor man’s Bayesian):不涉及marginalization,仅是一种按后验概率最大化的point estimate。这里的MAP(poor man’s Bayesian)是属于 点概率估计的。而全贝叶斯可以看作对test样本的所有参数集合的加权平均,PRML说的Bayesian主要还是指Empirical Bayesian:
Image may be NSFW.
Clik here to view.
这里的Image may be NSFW.
Clik here to view. 为超参 。
为超参 。
Curve fitting为例子:
1) MLE,直接对likelihood function求最大值,得到参数w。该方法属于point estimate。
2) MAP (poor man’s bayes),引入prior probability,对posterior probability求最大值,得到w。MAP此时相当于在MLE的目标函数(likelihood function)中加入一个L2 penalty。该方法仍属于point estimation。
3) fully Bayesian approach,需使用sum rule和product rule(因为“degree of belief”的machinery和概率相同,因此这两个rule对“degree of belief”成立),而要获得predictive distribution又需要marginalize (sum or integrate) over the whole of parameter space w:
Image may be NSFW.
Clik here to view.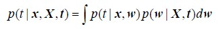
其中,x是待预测的点,X是观察到的数据集,t是数据集中每个数据点相应的label。其实是用参数w的后验概率为权,对probability进行一次加权平均;因此这个过程需要对w进行积分,即marginalization。
由于 marginalization 通常是非常难求取的,所以一般在针对Graphical Model的时候就需做Laplace approximation、Variation inference、MCMC采样这些。
所以我们要建立的概念是:Graphical Model的东西是一个需要marginalization的。
下面我们看看本讲的内容:
首先将上节 LS(Least Square)方法直接用于求分类问题,就可以得到 Least squares for classification。
Image may be NSFW.
Clik here to view.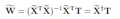 Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.
一般线性模型Generalized Linear Model: an activation function acting on a linear function of the feature variables:
Image may be NSFW.
Clik here to view.
Linear Model对于回归和分类的区别在于:激活函数的不同
Image may be NSFW.
Clik here to view.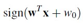
这里sign就是一个非线性的函数,其实是一个间断函数,非连续的。
下图证明了点到平面的距离公式。超平面:在一个D维Euclidean space中的超平面是一它的一个D-1维流形,而且该空间是一个线性空间。Linearly separable:分布于D维空间中的全部数据点可以用超平面无错地分隔成类。Coding scheme:1-of-K binary coding scheme,即如果有K个类,某数据点属于第i个类,则表示为一个K维向量,该向量除了第i个分量是1,其余都是0。
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.
关于超平面,线性可分的一些概念,在多类情况,可以使用1对1,1对多分类器的方式,例如:
你要分类3类物体: 苹果,西瓜,香蕉
那么 1对1 就是建立6个分类器
那么 1对1 就是建立3个分类器
苹果,西瓜
苹果,香蕉
西瓜,香蕉
1对多分类器就是:
苹果和非苹果
西瓜和非西瓜
香蕉和非香蕉
Image may be NSFW.
Clik here to view.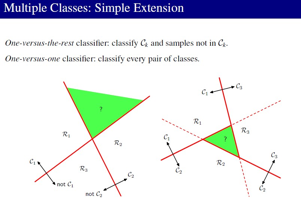
左边是1对多,右边是1对1,都存在一些无法分类的情况,也就是绿色区域部分。
多分类的决策域是单连通,而且是凸的, 下面给出了证明:
Image may be NSFW.
Clik here to view.
证明的图形示意:
Image may be NSFW.
Clik here to view.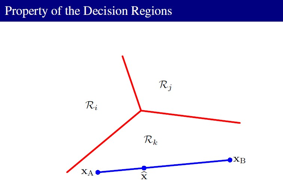
上面有没有问题?没有就继续讲 Fisher’s Linear Discriminant了。
echo<echotooo@gmail.com> 20:26:46
无法分类的情况一般怎么办?就是绿色区域了
planktonli(1027753147) 20:27:35
恩,那就是可能出现判断错误了,这个没有办法。
echo<echotooo@gmail.com> 20:28:12
哦,好的,pass。
planktonli(1027753147) 20:28:54
好了,现在看看 Fisher’s Linear Discriminant,Linear Discriminant Analysis, LDA),也叫做Fisher线性判别,这个要和Graphical Model的 Latent Dirichlet allocation 区分开。我个人认为 LDA可以看成一个有监督降维的东西,这些PCA(主成分分析),ICA(独立成分分析)也是降低维的,不过是无监督的东西,包括mainfold dimension reduction的,都是无监督的。LDA是降低到一个投影方向上,使得它的可分性最好
而PCA是要找它的主要成分也就是使得Loss最小的方向,LDA要求 类间散度最大,类内聚合度最强。
Image may be NSFW.
Clik here to view.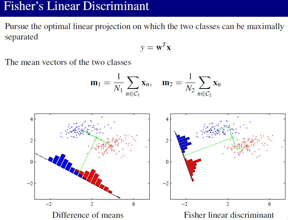
类间散度最大是通过它们的均值距离体现的,而 类内聚合度最强 是通过 类内的点到均值的散的程度表达的,也就是说Fisher分类是LS的特例,好了,看大家对 Fisher 还有什么疑问?
echo<echotooo@gmail.com> 20:41:53
….LDA是基于高斯分布假设上的吗?
planktonli(1027753147) 20:44:12
LDA的样本是需要在 Gaussian假设下,会有 power performance的,如果data 的distribution是非常不规则的,那么LDA肯定是失效的。那就需要用些 Kernel等的trick了。
echo<echotooo@gmail.com> 20:45:29
这是为什么,是因为它的公式推导的时候有用到高斯分布的假设吗?
planktonli(1027753147) 20:45:32
推导不需要Gaussian假设
网络上的尼采(813394698) 20:46:01
用到了均值
echo<echotooo@gmail.com> 20:46:40
协方差部分呢?
planktonli(1027753147) 20:47:00
需要两类的 Between class Variance,这个是通过 均值差表达的。
echo<echotooo@gmail.com> 20:47:28
嗯嗯,好像懂了,谢谢。
planktonli(1027753147) 20:47:45
如果两个类的mean完全相等,那么LDA肯定是失效的。if the distribution of data is not so good, then we may use Kernel Fisher discriminant analysis
I mean that the distribution doesn’t meet the gaussian。
echo<echotooo@gmail.com> 20:50:35
难道kfda不对高斯分布有偏好吗?
planktonli(1027753147) 20:50:42
the detail info you can c the web site http://en.wikipedia.org/wiki/Kernel_Fisher_discriminant_analysis KDA算法步聚,大部分跟LDA相同,不同的地方是用到了Kernel方法构造了矩阵Sb, Sw,这里的KDA就是kernel fisher 了。
电闪雷鸣(37633749) 20:52:11
OK,明白
planktonli(1027753147) 20:52:24
好了,下面看看NN神经网络的perceptron ,这个是一个单层的东西,注意它的training error函数 ,优化过程用的是梯度下降法:
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.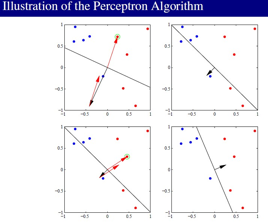 Image may be NSFW.
Image may be NSFW.
Clik here to view.
好了,perceptron是比较简单的。
下面看,Probabilistic Generative Models,通过MAP方式建立概率模型,需要 先验概率,类条件概率和边缘概率。2类的Probabilistic Generative Models就是 logistic sigmoid function:
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.
这种方法需要假设input的分布,即得到class-conditional distribution,用贝叶斯定理转化成后验概率后,就是和Discriminant model一样进行make decision了。
Image may be NSFW.
Clik here to view.
在gaussian分布的情况下,我们分析:
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.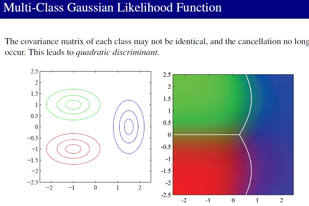
协方差矩阵不同,则变成了2次分类了,在2类情况下,我们用MLE方法,估计参数:
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.
步骤小结:
1) 假定class-conditional distribution的分布形式,MLE估计该分布中的参数(从而得到了class-conditional distribution)
2) 计算每个类别的后验概率。在上面的例子中,得到的后验概率刚好是一个GLM模型(Logistic)
好了,这部分结束了。大家讨论下,没问题就继续了。
Probabilistic Discriminative Models:
直接建立分类函数模型,而不是建立生成过程模型,生成模型和判别模型的区别:
maping the data from the orginal sapce to a new space may make it linearly separable
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.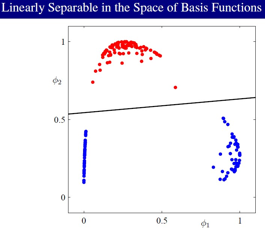 Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.
逻辑回归的最大似然参数估计方法:
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.
注意这里 ,Logistic regression是用于分类的,而不是回归。
好了,这就是Probabilistic Discriminative Models的内容,其实质还是 point estimization。
最后看看Bayesian Logistic Regression:
这里是 we want to approximate the posterior using Gaussian,就是用高斯分布近似后验概率
来看Laplace Approximation :
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.
Laplace近似将任意一个分布近似成了高斯分布
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.
好了,最后的 Bayesian Logistic Regression 也完了。
============================讨论=================================
zeno(117127143) 21:25:06
没太明白 ,生成模型和判别模型的区别 ,优缺点呢 ?
planktonli(1027753147) 21:26:02
一个model p(x,y) 生成式的,一个model p(y|X)判别式的,判别式的只在乎boundry的这些点,生成式的需要知道这些点是怎么生成的:
Image may be NSFW.
Clik here to view.
zeno(117127143) 21:26:38
是判别式要好一点吗 ?
planktonli(1027753147) 21:27:34
生成模型: Naive Bayes, Graphical Model ,判别模型: NN,SVM,LDA,Decision Tree 等。不能说谁好谁不好,还有 生成模型 + 判别模型的,例如: SVM的kernel construcion你可以用 generative的方式去做,那就是 Generative + Discriminant 的了。
zeno(117127143) 21:30:38
生成式要求X互相独立吧 ?
planktonli(1027753147) 21:31:39
恩,生成式是需要IID的,这个在statistics上通常都有IID假设的,否则不好整,还有什么问题?
HX(458728037) 21:33:12
我想问一个简单的问题,其实生成模型最后做分类的时候不还是根据一个boundary来判断的吗?
planktonli(1027753147) 21:34:32
生成模型 在 two class 而且是 gaussian distribution的时候,就可以转化为 判别式的,这个验证起来很简单,看看下面的PPT就明白了:
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.
zeno(117127143) 21:36:52
好的,谢谢,总是看见生成判别,弄不太清楚,关键是强调分清楚生成判别,对解决问题选那种工具有何影响,一直搞不清,我感觉feature 不独立时用判别,feature 多时用判别,那么生成式有什么优势呢?
阳阳(236995728) 21:34:22
判别模型用的是频率学派的观点 ,也就是最大似然估计法, 生成模型用的是贝叶斯学派观点 ,也就是最大后验概率。
planktonli(1027753147) 21:37:10
阳阳,这个是不对的。MLE也是statistics的东西,判别模型则根本不考虑 statistics,你可以看看NN的东西,包括今天的LDA,它们直接求boundry的。
晴(498290717) 21:39:41
查了下别人的博客,我觉得这个是两者最最本质的区别
Image may be NSFW.
Clik here to view. Image may be NSFW.
Image may be NSFW.
Clik here to view.
ant/wxony(824976094) 21:42:18
产生式模型和判别式模型我觉得就是把人的知识用在模型的构建还是feature的设计上,特征多的时候一般还是判别式模型猛些。
HX(458728037) 21:44:51
生成式的模型在无监督的一些学习上应该才好用吧 ?
ant/wxony(824976094) 21:45:43
嗯,无监督学习上确实
planktonli(1027753147) 21:48:38
我把 Generative verses discriminative classifier的一个PPT发到群里,大家有兴趣的看看:
“Lecture2.pdf” 下载
注:PRML读书会系列文章由 @Nietzsche_复杂网络机器学习 同学授权发布,转载请注明原作者和相关的主讲人,谢谢。
本文链接地址:http://www.52nlp.cn/prml读书会第四章-linear-models-for-classification