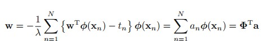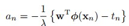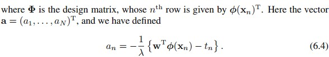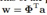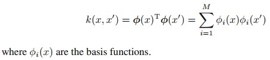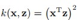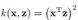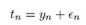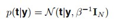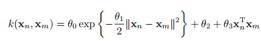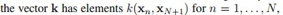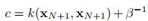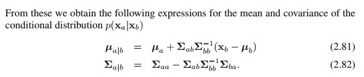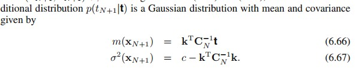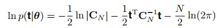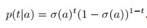PRML读书会第六章 Kernel Methods
主讲人 网络上的尼采
（新浪微博:@Nietzsche_复杂网络机器学习）
网络上的尼采(813394698) 9:16:05
今天的主要内容：Kernel的基本知识，高斯过程。边思考边打字，有点慢，各位稍安勿躁。
机器学习里面对待训练数据有的是训练完得到参数后就可以抛弃了，比如神经网络；有的是还需要原来的训练数据比如KNN，SVM也需要保留一部分数据–支持向量。
很多线性参数模型都可以通过dual representation的形式表达为核函数的形式。所谓线性参数模型是通过非线性的基函数的线性组合来表达非线性的东西，模型还是线性的。比如线性回归模型是y=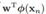
，
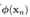是一组非线性基函数，我们可以通过线性的模型来表达非线性的结构。
核函数的形式：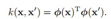
，也就是映射后高维特征空间的内积可以通过原来低维的特征得到。因此kernel methods用途广泛。
核函数有很多种，有平移不变的stationary kernels 
还有仅依赖欧氏距离的径向基核：
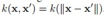
非线性转化为线性的形式的好处不言而喻，各种变换推导、闭式解就出来了。 下面推导下线性回归模型的dual representation，有助于我们理解核函数的作用：
根据最小二乘，我们得到下面的目标函数
，加了L2正则。我们对w求导，令J(w)的梯度等于0，得到以下解：
是个由基函数构成的样本矩阵，
向量里面的元素由
组成：
我们把
代入最初的J(w)得到：
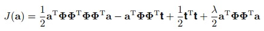
咱们用核矩阵K来替换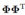
，其中矩阵K里面的元素是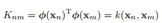
于是得到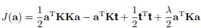
然后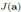
对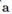求导，令其梯度等于0，得到解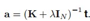
所以原来的线性回归方程就变成了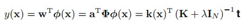
K(X)的含义：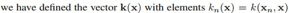
，上面的DUAL形式的含义非常明显，就是根据已知的的训练数据来做预测。至此原来线性回归方程的参数w消失，由核函数来表示回归方程，以上方式把基于特征的学习转换成了基于样本的学习。 这是线性回归的DUAL表示，svm等很多模型都有DUAL表示。
80(850639048) 10:09:50
professor 核函数其实是为了求基函数的内积对吗？
网络上的尼采(813394698) 10:12:57
如果有很多基的话维度势必会很高，计算内积的花销会很大，有些是无限维的，核函数能绕过高维的内积计算，直接用核函数得到内积。
接下来看下核函数的性质及构造方法。核函数的一般形式：
下面是个简单的例子说明
为什么是个核函数：
很明显 
是个核函数，它能写成核函数的一般形式。
核函数的一个充分必要定理也就是mercer定理：核矩阵是半正定的：
我们可以通过以下规则用简单的核函数来构造复杂的核函数：
过会我们讲高斯过程时再举个核函数线性组合的例子。
介绍一个经常用到的径向基核函数，高斯核：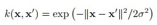
，这个核函数能把数据映射到无限维的空间：
中间
可以展开成无限维的，然后核函数可以表示成内积的形式。
内积的含义就是表示相似性，所以核函数还有其他的用法。比如我们可以通过生成模型来构造核。
两个变量的概率都很高相似性就越大，其实这样做就是映射到一维的内积。
我们可以引入离散的隐变量：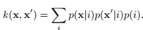
连续的隐变量：
举个这样做有啥用的例子，我们可以用来比较HMM由同一条隐马尔科夫链生成的两条序列的相似性：
网络上的尼采(813394698) 10:40:34
接下来讲我们今天的重点Gaussian Processes
牧云(1106207961) 10:41:02
数据海洋(1009129701) 10:41:14
我先再理解，理解这些。
网络上的尼采(813394698) 10:42:41
Gaussian Processes是贝叶斯学派的一个大杀器，用处很广。不同于参数模型，Gaussian Processes认为函数在函数空间里存在一个先验分布。
高斯过程和很多模型是等价的：ARMA (autoregressive moving average) models, Kalman filters, radial basis function networks ，还有特定情况下的神经网络。
现在我们从贝叶斯线性回归自然的引出高斯过程：
前面我们提到的线性回归的形式 
贝叶斯方法为参数加了一个高斯分布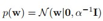 
大家发现了没有，这样做直接导致了函数有个预测分布，并且也是高斯的，因为方程是线性的并且参数是高斯分布。线性的东西和高斯分布总是不分家的。
我们定义向量：y，
y就是个多元的高斯分布。
它的每一维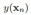 
都是个高斯分布，这也是高斯过程的由来。
y可以表示为 
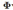是基函数组成的样本矩阵。
高斯过程可以由均值和协方差矩阵完全决定。由于w的均值是0，所以我们也认为高斯过程的均值是0，
剩下的就是根据定义求它的协方差矩阵，很自然地就得出来了：
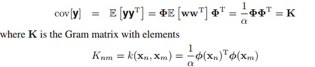
矩阵K里的元素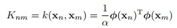
都是核函数的形式。
选用什么样的核函数也是问题，下面的图是对采用高斯核和指数核的高斯过程的取样，一共取了5条，可以看到两者的区别：
接下来我们就用GP来做回归 ：
我们观测的目标值是包含噪音的，噪音是高斯分布。
那么根据线性高斯模型的性质，
，其中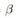
是噪音的参数
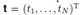对于向量
和向量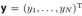
咱们前面说过了，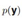
可以表示为
所以marginal distribution：
其中矩阵C的元素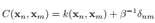
，
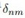是单位矩阵的元素，其实就是把
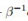加在了矩阵K的对角线上。这个不难理解，一开始
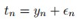，都是高斯的，协方差是两者的相加，噪音每次取都是独立的，所以只在协方差矩阵对角线上有。
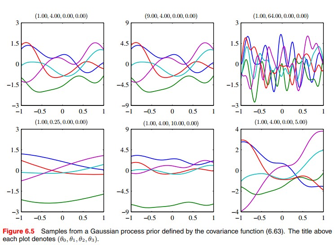
现在确定下用什么核的问题，举个例子，下面这个核函数用了高斯核，线性核，以及常数的线性组合，这样做是为了更灵活，过会再讲如何确定里面的这些超参：
下图是不同的超参对高斯过程的影响：
解决了核函数的问题，我们再回来，通过前面的结论，不难得出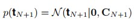 
如何确定矩阵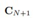
呢，其实我们在原来矩阵
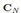的基础上补上就行。
k和c比较容易理解：
咱们的最终目标就是得
，由于这两个都是高斯分布，用第二章条件高斯分布的公式套一下，其中均值是0：
就会得到的均值和方差：
可以看出均值和方差都是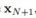
的函数，我们做预测时用均值就行了。
最后一个问题就是高斯过程是由它的协方差矩阵完全决定的，我们如何学习矩阵里面的超参呢？包括我们刚才提到的核函数里面的参数以及噪音的参数。
其实由于高斯分布的原因，我们可以方便的利用log最大似然：
求最优解时可以用共轭梯度等方法，梯度：
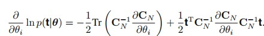
到这里，用高斯过程做回归就结束了。
有了做回归的基础，咱们再看下如何做分类。
类似逻辑回归，加个sigmoid函数就能做分类了：
分类与回归不同的是
是个伯努利分布。
这里还和前面一样。
对于二分类问题，最后我们要得到是：
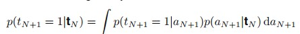
但是这个积分是不容易求的，
是伯努利分布，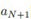
是高斯分布，不是共轭的。求积分的方法有很多，可以用MCMC，也可以用变分的方法。书上用的是Laplace approximation。
今天就到这里吧，我去吃饭，各位先讨论下吧。
上面Gaussian Processes的公式推导虽然有点多，但都是高斯分布所以并不复杂，并且GP在算法实现上也不难。
另外给大家推荐一个机器学习视频的网站，http://blog.videolectures.net/100-most-popular-machine-learning-talks-at-videolectures-net/ 里面有很多牛人比如Jordan的talks，第一个视频就是剑桥的David MacKay讲高斯过程，他的一本书 Information Theory, Inference and Learning Algorithms也很出名。
两栖动物(9219642) 14:35:09
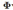是个由基函数构成的矩阵，向量a里面的元素由
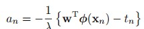组成。
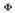的维度是基函数的个数，an的维度是样本的个数把?
网络上的尼采(813394698) 14:36:44
对
两栖动物(9219642) 14:37:48
哪这2个怎么后来乘在一起了？维度不是不一样吗？
网络上的尼采(813394698) 14:49:01
@两栖动物 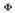不是方阵，可以相乘
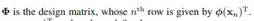
明白了吧，另外这个由基函数表示的样本矩阵只在推导里存在。
两栖动物(9219642) 14:56:08
明白了，谢谢
注：PRML读书会系列文章由 @Nietzsche_复杂网络机器学习 同学授权发布，转载请注明原作者和相关的主讲人，谢谢。
本文链接地址：http://www.52nlp.cn/prml读书会第六章-kernel-methods