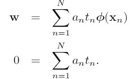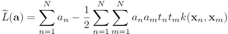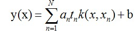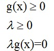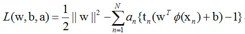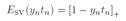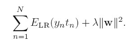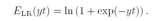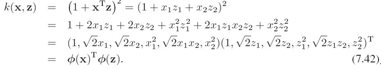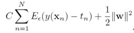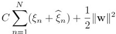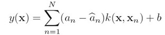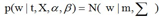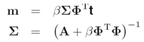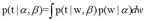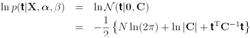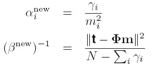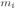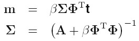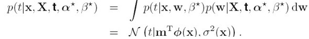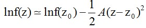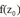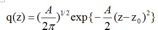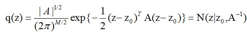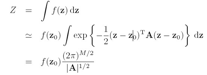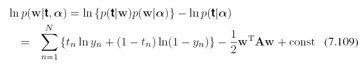PRML读书会第七章 Sparse Kernel Machines
主讲人 网神
(新浪微博: @豆角茄子麻酱凉面)
网神(66707180) 18:59:22
大家好,今天一起交流下PRML第7章。第六章核函数里提到,有一类机器学习算法,不是对参数做点估计或求其分布,而是保留训练样本,在预测阶段,计算待预测样本跟训练样本的相似性来做预测,例如KNN方法。
将线性模型转换成对偶形式,就可以利用核函数来计算相似性,同时避免了直接做高维度的向量内积运算。本章是稀疏向量机,同样基于核函数,用训练样本直接对新样本做预测,而且只使用了少量训练样本,所以具有稀疏性,叫sparse kernel machine。
本章包括SVM和RVM(revelance vector machine)两部分,首先讲SVM,支持向量机。首先看SVM用于二元分类,并先假设两类数据是线性可分的。
二元分类线性模型可以用这个式子表示: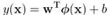 。其中
。其中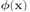 是基函数,这些都跟第三章和第四章是一样的。
是基函数,这些都跟第三章和第四章是一样的。
两类数据线性可分,当 时,分类结果是
时,分类结果是 ;
; 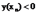 时,分类结果
时,分类结果 ;也就是对所有训练样本总是有
;也就是对所有训练样本总是有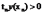 .要做的就是确定决策边界y(x)=0
.要做的就是确定决策边界y(x)=0
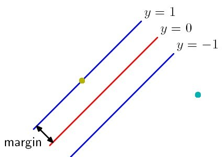
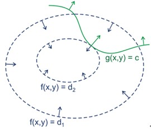
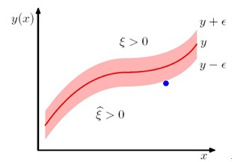
为了确定决策边界 ,SVM引入margin的概念。margin定义为决策边界y(x)到最近的样本的垂直距离。如下图所示:
,SVM引入margin的概念。margin定义为决策边界y(x)到最近的样本的垂直距离。如下图所示:
SVM的目标是寻找一个margin最大的决策边界。 我们来看如何确定目标函数:
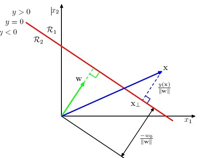
首先给出一个样本点x到决策边界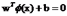 的垂直距离公式是什么,先给出答案:|y(x)|/||w||
的垂直距离公式是什么,先给出答案:|y(x)|/||w||
这个距离怎么来的,在第四章有具体介绍。看下图:
图例,我们看点x到y=0的距离r是多少:
上面我们得到了任意样本点x到y(x)=0的距离,要做的是最大化这个距离。
同时,要满足条件 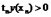
所以目标函数是:
求w和b,使所有样本中,与y=0距离最小的距离 最大化,整个式子就是最小距离最大化
这个函数优化很复杂,需要做一个转换
可以看到,对w和b进行缩放  ,距离
,距离  并不会变化
并不会变化
根据这个属性,调整w和b,使到决策面最近的点满足: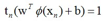
从而左右样本点都满足 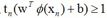
这样,前面的目标函数可以变为:
同时满足约束条件: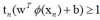
这是一个不等式约束的二次规划问题,用拉格朗日乘子法来求解
构造如下的拉格朗日函数: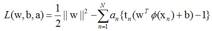
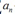 是拉格朗日乘子 ,这个函数分别对w和b求导,令导数等于0,可以得到w和b的表达式:
是拉格朗日乘子 ,这个函数分别对w和b求导,令导数等于0,可以得到w和b的表达式:
将w带入前面的拉格朗如函数L(w,b,a),就可以消去w和b,变成a的函数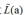 ,这个函数是拉格朗日函数的对偶函数:
,这个函数是拉格朗日函数的对偶函数:
为什么要转换成对偶函数,主要是变形后可以借助核函数,来解决线性不可分的问题,尤其是基函数的维度特别高的情况。求解这个对偶函数,得到参数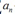 ,就确定了分类模型
,就确定了分类模型
把  带入
带入 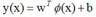 ,就是用核函数表示的分类模型:
,就是用核函数表示的分类模型:
这就是最终的分类模型,完全由训练样本 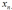 ,n=1…N决定。
,n=1…N决定。
SVM具有稀疏性,这里面对大部分训练样本,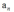 都等于0,从而大部分样本在新样本预测时都不起作用。
都等于0,从而大部分样本在新样本预测时都不起作用。
我们来看看为什么大部分训练样本,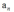 都等于0。这主要是由KKT条件决定的。我们从直观上看下KKT条件是怎么回事:
都等于0。这主要是由KKT条件决定的。我们从直观上看下KKT条件是怎么回事:
KKT是对拉格朗日乘子法的扩展,将其从约束为等式的情况扩展为约束为不等式的情况。所以先看下约束为等式的情况:例如求函数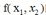 的极大值,同时满足约束
的极大值,同时满足约束  ,拉格朗日乘子法前面已经介绍,引入拉式乘子,构造拉式函数,然后求导,解除的值就是极值。这里从直观上看一下,为什么这个值就是满足条件的极值。设想取不同的z值,使
,拉格朗日乘子法前面已经介绍,引入拉式乘子,构造拉式函数,然后求导,解除的值就是极值。这里从直观上看一下,为什么这个值就是满足条件的极值。设想取不同的z值,使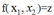 ,就可以得到f(x1,x2)的不同等高线,如图:
,就可以得到f(x1,x2)的不同等高线,如图:
构成图中的曲线,图中标记的g=c,对于这种情况,改成g-c=0就可以了.假设g与f的某些等高线相交,交点就是同时满足约束条件和目标函数的值,但不一定是极大值。。有两种相交形式,一种是穿过,一种是相切。因为穿过意味着在该条等高线内部还存在着其他等高线与g相交,新等高线与目标函数的交点的值更大。只有相切时,才可能取得最大值。因此,在极大值处,f的梯度与g的梯度是平行的,因为梯度都垂直于g或f曲线,也就是存在lamda,使得 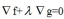 ,这个式子正是拉格朗日函数
,这个式子正是拉格朗日函数 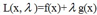 对x求导的结果。
对x求导的结果。
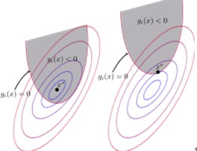
接下来看看约束条件为不等式的情况,例如约束为 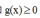 ,先看个图:
,先看个图:
图里的约束是g<0,不影响解释KKT条件。不等式约束分两种情况,假设极值点是x` ,当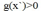 时,也就是图中左边那部分,此时该约束条件是inactive的,对于极值点的确定不起作用。因此拉格朗日函数
时,也就是图中左边那部分,此时该约束条件是inactive的,对于极值点的确定不起作用。因此拉格朗日函数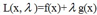 中,lamda等于0,极值完全由f一个人确定,相当于lamda等于0.当
中,lamda等于0,极值完全由f一个人确定,相当于lamda等于0.当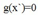 时,也就是图中右边部分,极值出现在g的边界处,这跟约束条件为等式时是一样的。
时,也就是图中右边部分,极值出现在g的边界处,这跟约束条件为等式时是一样的。
总之,对于约束条件为不等式的拉格朗日乘子法,总有 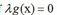 ,不是lamda等于0,就是g=0
,不是lamda等于0,就是g=0
这个结论叫KKT条件,总结起来就是:
再返回来看SVM的目标函数构造的拉格朗日函数:
根据KKT条件,有 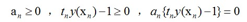 ,所以对于
,所以对于 大于1的那些样本点,其对应
大于1的那些样本点,其对应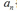 的都等于0。只有
的都等于0。只有 等于1的那些样本点对保留下来,这些点就是支持向量。
等于1的那些样本点对保留下来,这些点就是支持向量。
这部分大家有什么意见和问题吗?
============================讨论===============================
Fire(564122106) 20:01:56
他为什么要符合KKT条件啊
网神(66707180) 20:02:33
因为只有符合KKT条件,才能有解,否则拉格朗日函数没解,我的理解是这样的
Fire(564122106) 20:03:54
我上次看到一个版本说只有符合KKT条件 对偶解才和原始解才相同,不知道怎么解释。
kxkr<lxfkxkr@126.com> 20:04:18
貌似统计学习方法 附录里面 讲了这个
Wolf <wuwja@foxmail.com> 20:04:19
an为0为什么和kkt条件相关
kxkr<lxfkxkr@126.com> 20:04:20
不过忘记了 ,我上次看到一个版本说只有符合KKT条件,对偶解才和原始解相同。
YYKuaiXian(335015891) 20:04:40
Ng的讲义就是用这种说法
苦瓜炒鸡蛋(852383636) 20:04:47
因为大部分的样本都不是sv
Wolf <wuwja@foxmail.com> 20:05:05
如果两类正好分布在margin上,那么所有的点都是sv
YYKuaiXian(335015891) 20:05:40
Wolf <wuwja@foxmail.com> 20:05:54
只有符合kkt条件,primary问题和due问题的解才是一样的,否则胖子里面的瘦子总比瘦子里面的胖子大。
kxkr<lxfkxkr@126.com> 20:07:03
这个比喻 好!
高老头(1316103319) 20:07:08
对偶问题和原问题是什么关系,一个问题怎么找到它的对偶问题?
Wolf <wuwja@foxmail.com> 20:07:19
所以kkt条件和sv为什么大部分为0没有直接关系,sv为0个人觉得是分界面的性质决定的,分界面是一个低维流形。
Fire(564122106) 20:08:38
我也感觉sv是和样本数据性质有关的
Wolf <wuwja@foxmail.com> 20:09:26
比如在二维的时候,分界面是一个线性函数,导致sv比较少,当投影到高维空间,分界面变成了一个超平面,导致sv变多了,另外,很多样本变成sv也是svm慢的一个原因。
网神(66707180) 20:09:37
sv本质上是svm选择的错误函数决定的,在正确一边分类边界以外的样本点,错误为0,在边界以内或在错误一边,错误大于0.
苦瓜炒鸡蛋(852383636) 20:11:04
sv确定的超平面 而非是超平面确定的sv
Wolf <wuwja@foxmail.com> 20:11:30
sv确定的超平面 而非是超平面确定的sv,一样的,hinge为什么会导致稀疏?什么样的优化问题才有对偶问题,我也在疑问。对于一些规划问题(线性规划,二次规划)可以将求最大值(最小值)的问题转化为求最小值最大值的问题。
网神(66707180) 20:12:24
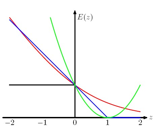
kkt是从一个侧面解释稀疏,从另一个侧面,也就是错误函数是hinge函数,也可以得出稀疏的性质。svm跟逻辑回归做对比, hinge损失导致稀疏,我们先讲下这吧,svm的错误函数可以这么写:
这就是hinge错误函数,图形如图中的蓝色线
而逻辑回归的错误函数是:
如图中的红色线,红色线跟蓝色线走势相近 ,区别是hinge函数在 ,图中z>1时,错误等于0,也就是yt>1的那些点都不产生损失. 这个性质可以带来稀疏的解。
,图中z>1时,错误等于0,也就是yt>1的那些点都不产生损失. 这个性质可以带来稀疏的解。
========================讨论结束===============================
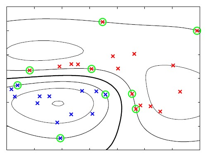
我接着讲了,后面还有挺多内容,刚才说的都是两类训练样本可以完全分开的情况,比如下面这个图,采用了高斯核函数的支持向量机,可以很清楚的看到决策边界,支持向量:
但实际中两类数据的分布会有重叠的情况,另外也有噪音的存在,导致两类训练数据如果一定要完全分开,泛化性能会很差。因此svm引入一些机制,允许训练时一些样本被误分类.我们要修改目标函数,允许样本点位于错误的一边,但会增加一个惩罚项,其大小随着数据点到边界的距离而增大这个惩罚项叫松弛变量, slack variables,记为 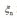 ,并且大于等于0.其中下标n=1,..,N,也就是每个训练样本对应一个
,并且大于等于0.其中下标n=1,..,N,也就是每个训练样本对应一个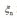 ,对于位于正确的margin边界上或以内的数据点,其松弛变量
,对于位于正确的margin边界上或以内的数据点,其松弛变量 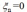 ,其他样本点
,其他样本点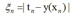
这样,如果样本点位于决策边界y(x)=0上, 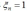
如果被错分,位于错误的一边, 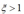 ,因此目标函数的限制条件由
,因此目标函数的限制条件由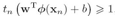 修改为
修改为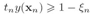 ,目标函数修从最小化
,目标函数修从最小化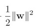 改为最小化
改为最小化 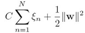 ,其中参数C用于控制松弛变量和margin之间的trade-off,因为对于错分的点,有
,其中参数C用于控制松弛变量和margin之间的trade-off,因为对于错分的点,有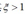 ,所以
,所以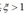 是错分样本数的一个上限upper bound ,所以C相当于一个正则稀疏,控制着最小错分数和模型复杂度的trade-off.
是错分样本数的一个上限upper bound ,所以C相当于一个正则稀疏,控制着最小错分数和模型复杂度的trade-off.
SVM在实际使用中,需要调整的参数很少,C是其中之一。
看这个目标函数,可以看到,C越大,松弛变量就越倍惩罚,就会训练出越复杂的模型,来保证尽量少的样本被错分。当C趋于无穷时,每个样本点就会被模型正确分类。
我们现在求解这个新的目标函数,加上约束条件,拉格朗日函数如下:
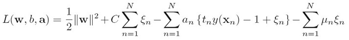
其中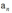 和
和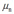 是拉式乘子,分别对w, b和{
是拉式乘子,分别对w, b和{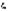 }求导,令导数等于0,得到w, b,
}求导,令导数等于0,得到w, b,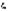 的表示,带入L(w,b,a),消去这些变量,得到以拉格朗日乘子为变量的对偶函数:
的表示,带入L(w,b,a),消去这些变量,得到以拉格朗日乘子为变量的对偶函数:
新的对偶函数跟前面的对偶函数形式相同,只有约束条件有不同。 这就是正则化的SVM。
接下来提一下对偶函数的解法,对偶函数都是二次函数,而且是凸函数,这是svm的优势,具有全局最优解,该二次规划问题的求解难度是参数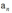 的数量很大,等于训练样本的数量 。书上回顾了一些方法,介绍不详细,主要思想是chunking,我总结一下,总结的不一定准确:
的数量很大,等于训练样本的数量 。书上回顾了一些方法,介绍不详细,主要思想是chunking,我总结一下,总结的不一定准确:
1.去掉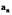 =0对应的核函数矩阵的行和列,将二次优化问题划分成多个小的优化问题;
=0对应的核函数矩阵的行和列,将二次优化问题划分成多个小的优化问题;
2.按固定大小划分成小的优化问题。
3.SVM中最流行的是SMO, sequentialminimal optimization。每次只考虑两个拉格朗日乘子.
SVM中维度灾难问题:核函数相当于高维(甚至无线维)的特征空间的内积,避免了显示的高维空间运算,貌似是避免了维度过高引起的维度灾难问题。 但实际上并没有避免。书上举了个例子 ,看这个二维多项式核函数:
这个核函数表示一个六维空间的内积。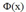 是从输入空间到六维空间的映射.映射后,六个维度每个维度的值是由固定参数的,也就是映射后,六维特征是有固定的形式。因此,原二维数据x都被限制到了六维空间的一个nonlinear manifold中。这个manifold之外就没有数据.
是从输入空间到六维空间的映射.映射后,六个维度每个维度的值是由固定参数的,也就是映射后,六维特征是有固定的形式。因此,原二维数据x都被限制到了六维空间的一个nonlinear manifold中。这个manifold之外就没有数据.
网神(66707180) 20:48:59
大家有什么问题吗?
高老头(1316103319) 20:49:58
manifold是什么意思?
网神(66707180) 20:50:26
我的理解是空间里一个特定的区域,原空间的数据,如果采样不够均匀,映射后的空间,仍然不会均匀,不会被打散到空间的各个角落,而只会聚集在某个区域。
接下来讲下SVM用于回归问题.
在线性回归中,一个正则化错误函数如下:
为了获得稀疏解,将前面的二次错误函数用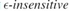 错误函数代替
错误函数代替
这个错误函数在y(x)和t的差小于时等于0.错误函数变为:
我们再引入松弛变量,对每个样本,有两个松弛变量,分别对应 
如图:
没引入松弛变量前,样本值t预测正确的条件是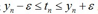
引入松弛变量后,变为: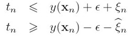
错误函数变为:
加上约束条件 ,就可以写出拉格朗日函数
,就可以写出拉格朗日函数
下面就跟前面的分类一样了.
关于统计学习理论,书上简单提了一下PAC(probably approximately correct)和VC维,简单总结一下书上的内容:PAC的目的是理解多大的数据集可以给出好的泛化性,以及研究损失的上限。PAC里的一个关键概念是VC维,用于提供一个函数空间复杂度的度量,将PAC理论推广到了无限大的函数空间上。
============================讨论===============================
Fire(564122106) 21:05:56
有哪位大神想过对svm提速的啊,svm在非线性大数据的情况下,速度还是比较慢的啊
网神(66707180) 21:07:36
svm分布式训练的方案研究过吗?
Fire(564122106) 21:09:29
没有,不过将来肯定要研究的!现在只是单机,现在有在单机的情况下,分布式进入内存的方案,有兴趣的可以看下:Selective Block Minimization for Faster Convergence of Limited Memory Large_Scale Linear Models 这个有介绍,我共享下啊。
苦瓜炒鸡蛋(852383636) 21:11:05
韩家炜的一个学生 提出了一个 仿照层次聚类的思想 改进的svm 速度好像挺快的
Making SVMs Scalable to Large Data Sets using Hierarchical Cluster Indexing 这个就是那篇论文的题目 发在 Data Mining and Knowledge Discovery
Fire(564122106) 21:16:29
哦 我看下,我现在看的都是台湾林的
Fire 分享文件 21:14:33
“Selective Block Minimization for Faster Convergence of Limited Memory Large_Scale Linear Models.pdf” 下载
苦瓜炒鸡蛋(852383636) 21:17:41
有那个大神 在用svm做聚类,Support Vector Clustering 这篇能做 就是时间复杂度太高了
========================讨论结束===============================
网神(66707180) 8:54:01
咱们开始讲RVM,前面讲了SVM,SVM有一些缺点,比如输出是decision而不是概率分布,SVM是为二元分类设计的,多类别分类不太实用,虽然有不少策略可以用于多元分类,但也各有问题参数C需要人工选择,通过多次训练来调整,感觉实际应用中这些缺点不算什么大缺点,但是RVM可以避免这些缺点。
RVM是一种贝叶斯方式的稀疏核方法,可以用于回归和分类,除了避免SVM的主要缺点,还可以更稀疏,而泛化能力不会降低 。先看RVM回归,RVM回归的模型跟前面第三章形式相同,属于线性模型,但是参数w的先验分布有所不同。
这个不同导致了稀疏性,等下再看这个不同
线性回归模型如下: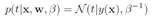
其中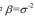 ,是噪音的精度precision
,是噪音的精度precision
均值y(x)定义为: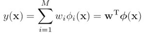
RVM作为一种稀疏核方法,它是如何跟核函数搭上边的,就是基函数 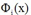 采用了核函数的形式
采用了核函数的形式
每个核与一个训练样本对应,也就是:

这个形式跟SVM用于回归的模型形式是相同的,看前面的式子(7.64)最后求得的SVM回归模型是:
可以看到,RVM回归和SVM回归模型相同,只是前面的系数从 ,接下来分析如何确定RVM模型中的参数w,下面的分析过程跟任何基函数都适用,不限于核函数。
,接下来分析如何确定RVM模型中的参数w,下面的分析过程跟任何基函数都适用,不限于核函数。
确定w的过程可以总结为:先假设w的先验分布,一般是高斯分布;然后给出似然函数,先验跟似然函数相乘的到w的后验分布,最大化后验分布,得到参数w 。
先看w的先验,w的先验是以0为均值,以 为精度的高斯分布,但是跟第三章线性回归的区别是,RVM为每个
为精度的高斯分布,但是跟第三章线性回归的区别是,RVM为每个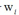 分别引入一个精度
分别引入一个精度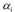 ,而不是
,而不是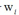 所有用一个的共享的精度
所有用一个的共享的精度
所以w的先验是:
对于线性回归模型,根据这个先验和似然函数可以得到其后验分布:
这是第三章的结论,推导过程就不说了
其中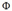 是NxM的矩阵,
是NxM的矩阵,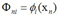 ,A是对角矩阵
,A是对角矩阵
对于RVM,因为基函数是核函数,所以 ,K是NxN维的核矩阵,其元素是
,K是NxN维的核矩阵,其元素是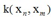
接下来需要确定超参数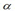 和
和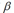 。一个是w先验的精度,一个是线性模型p(t|x,w)的精度
。一个是w先验的精度,一个是线性模型p(t|x,w)的精度
确定的方法叫做evidence approximation方法,又叫type-2 maximum likelihood,这在第三章有详细介绍,这里简单说一下思路:
该方法基于一个假设,即两个参数是的后验分布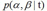 是sharply peaked的 ,其中心值是
是sharply peaked的 ,其中心值是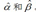 ,根据贝叶斯定理,
,根据贝叶斯定理, ,先验
,先验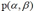 是relatively flat的,所以只要看
是relatively flat的,所以只要看 ,
,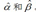 就是使的
就是使的 最大的值。
最大的值。
 是对w进行积分的边界分布:
是对w进行积分的边界分布:
这个分布是两个高斯分布的卷积,其log最大似然函数是:
其中C是NxN矩阵,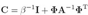
 这一步,以及C的值,是第三章的内容,大家看前面吧。
这一步,以及C的值,是第三章的内容,大家看前面吧。
我们可以通过最大化似然函数,求得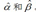 ,书上提到了两种方法,一种是EM,一种是直接求导迭代。前者第九章尼采已经讲了,这里看下后者。
,书上提到了两种方法,一种是EM,一种是直接求导迭代。前者第九章尼采已经讲了,这里看下后者。
首先我们分别求这个log似然函数对所有参数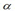 和
和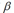 求偏导,并令偏导等于0,求得参数的表达式:
求偏导,并令偏导等于0,求得参数的表达式:
 是度量
是度量 被样本集合影响的程度
被样本集合影响的程度
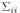 是w的后验方差
是w的后验方差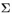 的对角线上的元素。
的对角线上的元素。
求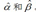 是一个迭代的过程:
是一个迭代的过程:
先选一个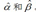 的初值,然后用下面这个公式得到后验的均值和方差:
的初值,然后用下面这个公式得到后验的均值和方差:
这样迭代计算,一直到到达一个人为确定的收敛条件,这就是确定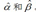 的过程。
的过程。
通过计算,最后的结果中,大部分参数 都是非常大甚至无穷大的值,从而根据w后验均值和方差的公式,其均值和方差都等于0,这样
都是非常大甚至无穷大的值,从而根据w后验均值和方差的公式,其均值和方差都等于0,这样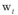 的值就是0,其对应的基函数就不起作用了 ,从而达到了稀疏的目的。这就是RVM稀疏的原因。
的值就是0,其对应的基函数就不起作用了 ,从而达到了稀疏的目的。这就是RVM稀疏的原因。
需要实际推导一下整个过程,才能明白为什么大部分 都趋于无穷大。那些
都趋于无穷大。那些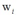 不为0的
不为0的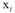 叫做relevance vectors,相当于SVM中的支持向量。需要强调,这种获得稀疏性的机制可以用于任何基函数的线性组合中。这种获得稀疏性的机制似乎非常普遍的。
叫做relevance vectors,相当于SVM中的支持向量。需要强调,这种获得稀疏性的机制可以用于任何基函数的线性组合中。这种获得稀疏性的机制似乎非常普遍的。
求得超参数,就可以通过下面式子得到新样本的分布:
下面看一个图示:
可以看到,其相关向量的数量比SVM少了很多,跟SVM相比的缺点是,RVM的优化函数不是凸函数,训练时间比SVM长,书上接下来专门对RVM的稀疏性进行分析,并且介绍了一种更快的求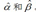 的方法:
的方法:
我接着讲RVM分类,我们看逻辑回归分类的模型:
 是sigmoid函数,我们引入w的先验分布,跟RVM回归相同,每个
是sigmoid函数,我们引入w的先验分布,跟RVM回归相同,每个 对应一个不同的精度
对应一个不同的精度
这种先验叫做ARD先验,跟RVM回归相比,在求 的分布时,不再对w进行积分。
的分布时,不再对w进行积分。
我们看在RVM回归时,是这么求 的:
的:
从而得到:
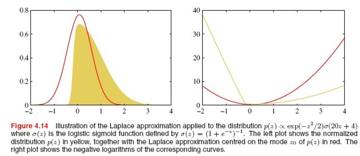
在RVM分类时,因为涉用到sigmod函数,计算积分很难,具体的为什么难,在第四章4.5节有更多的介绍,我们这里用Laplace approximation来求 的近似高斯分布,Laplace approximation我叫拉普拉斯近似,后面都写中文了。
的近似高斯分布,Laplace approximation我叫拉普拉斯近似,后面都写中文了。
先看下拉普拉斯近似的原理,拉普拉斯近似的目的是找到连续变量的分布函数的高斯近似分布,也就是用高斯分布 近似模拟一个不是高斯分布的分布。
假设一个单变量z,其分布是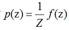 ,分母上的Z是归一化系数
,分母上的Z是归一化系数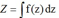 ,目标是找到一个可以近似p(z)的高斯分布q(z)。
,目标是找到一个可以近似p(z)的高斯分布q(z)。
第一步是先找到p(z)的mode(众数) ,众数mode是一个统计学的概念,可以代表一组数据,不受极端数据的影响,比如可以选择中位数做一组实数的众数,对于高斯分布,众数就是其峰值。一组数据可能没有众数也可能有几个众数。
拉普拉斯分布第一步要找到p(z)的众数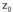 ,这是p(z)的一个极大值点,可能是局部的,因为p(z)可能有多个局部极大值。在该点,一阶导数等于0,
,这是p(z)的一个极大值点,可能是局部的,因为p(z)可能有多个局部极大值。在该点,一阶导数等于0,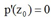 ,后面再说怎么找
,后面再说怎么找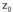 。找到
。找到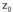 后,用
后,用 的泰勒展开来构造一个二次函数:
的泰勒展开来构造一个二次函数:
其中A是f(z)在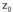 的二阶导数再取负数。上式中,没有一阶导数部分,因为
的二阶导数再取负数。上式中,没有一阶导数部分,因为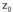 是局部极大值,一阶导数为0,把上式两边取指数,得到:
是局部极大值,一阶导数为0,把上式两边取指数,得到:
拉普拉斯分布得到的近似高斯分布的一个图示:
注意,高斯近似存在的条件是,原分布的二阶导数取负数、也就是高斯近似的精确度A>0,也就是驻点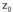 必须是局部极大值,f(x)在改点出的导数为负数。当z是一个M维向量时,近似方法跟单变量的不同只是二阶导数的负数A变成了MxM维的海森矩阵的负数。
必须是局部极大值,f(x)在改点出的导数为负数。当z是一个M维向量时,近似方法跟单变量的不同只是二阶导数的负数A变成了MxM维的海森矩阵的负数。
多维变量近似后的高斯分布如下:
A是海森矩阵的负数.mode众数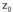 一般是通过数值优化算法来寻找的,不讲了。
一般是通过数值优化算法来寻找的,不讲了。
再回来看用拉普拉斯分布来近似RVM分类中的 :
:
刚才拉普拉斯分布忘了说一个公式,就是求得q(z)后,确定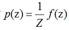 中的分母,也就是归一化系数的公式:
中的分母,也就是归一化系数的公式:
这个一会有用。先看RVM中对w的后验分布的近似,先求后验分布的mode众数,通过最大化log后验分布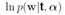 来求mode.先写出这个log后验分布:
来求mode.先写出这个log后验分布:
其中
最后求得的高斯近似的均值(也就是原分布的mode)和精度如下:
现在用这个w后验高斯近似来求边界似然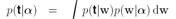
根据前面那个求归一化系数Z的公式Z=
有:
RVM这部分大量基于第二章高斯分布和第三、四两章,公式推导很多,需要前后关联才能看明白。
注:PRML读书会系列文章由 @Nietzsche_复杂网络机器学习 同学授权发布,转载请注明原作者和相关的主讲人,谢谢。
PRML读书会讲稿PDF版本以及更多资源下载地址:http://vdisk.weibo.com/u/1841149974
本文链接地址:http://www.52nlp.cn/prml读书会第七章-sparse-kernel-machines